Electric Flux

  • Electric Flux is the amount of electric field penetrating a surface

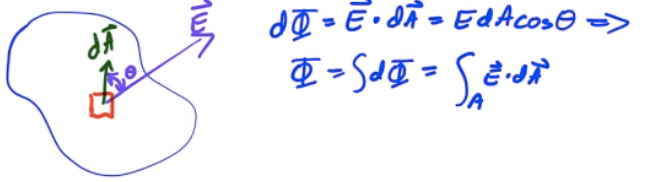
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image062.png

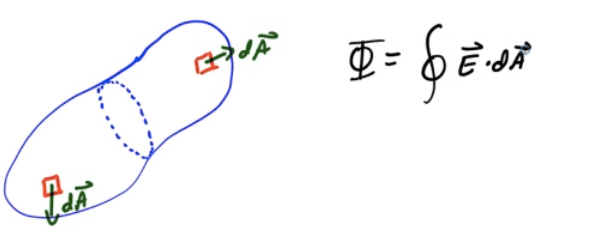
    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image063.png

Point Charge Inside a Hollow Sphere

  • Place a point charge inside a hollow sphere of radius R.

  • Determine the flux through the sphere

    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image064.png

Gauss's Law

  • Useful for finding the electric field due to charge distributions for cases of:

    • Spherical Symmetry

    • Cylindrical Symmetry

    • Planar Symmetry

    Gauss's Law for Electric Fields from Fleisch Reminder that the electric field is a vector Reminder that this integral is over a closed surface Dot product tells you to find the part of E parallel to h (perpendicular to the surface) The unit vector normal to the surface Electric Flux Tells you to sum up the The electric field in N/C An increment of surface area in m2 The amount of net charge in coulombs Reminder that only the enclosed charge contributes The electric permittivity of the free space contributions from each Reminder that this is a surface portion of the surface integral (not a volume or a line integral) The flux of an electric field passing through any closed surface is proportional to the total charge contained within that surface.

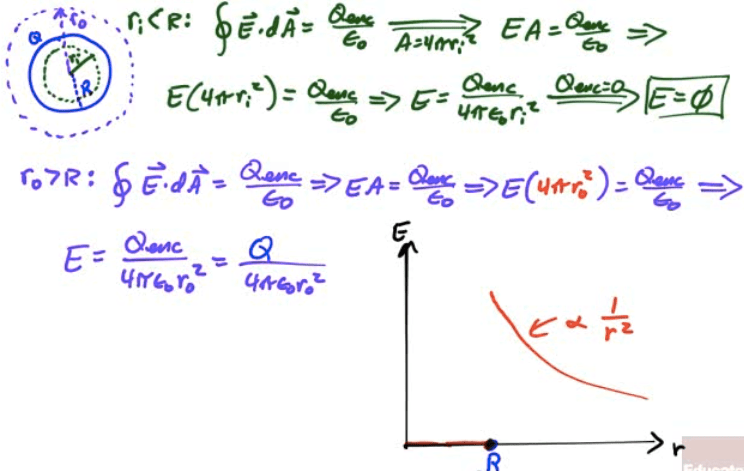
Practice Question 1

  • Find the electric field inside and outside a thin hollow shell of uniformly distributed charge Q

    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image066.png

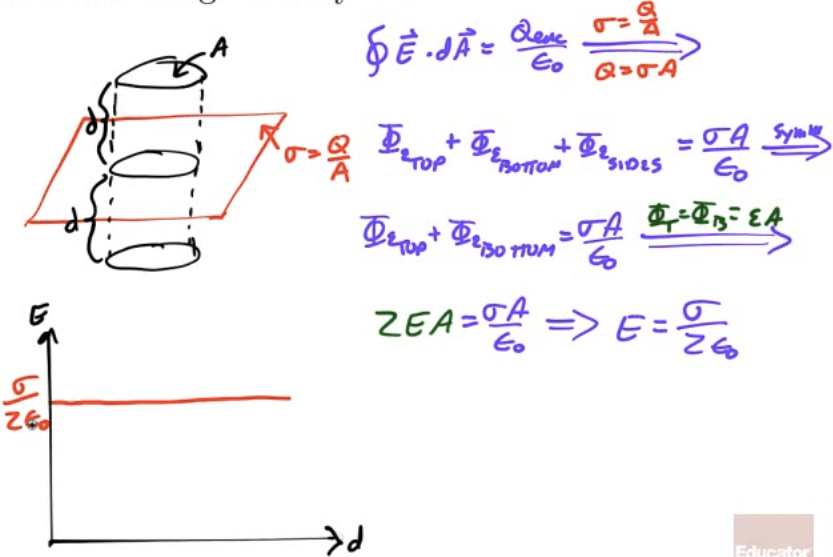
Practice Question 2

  • Find the electric field E to an infinite plane of uniform charge density σ.

    = ヨ く = = ゲ ヨ Z 0 ラ 0 レ -D 、 0 ラ 代 ヨ

Practice Question 3

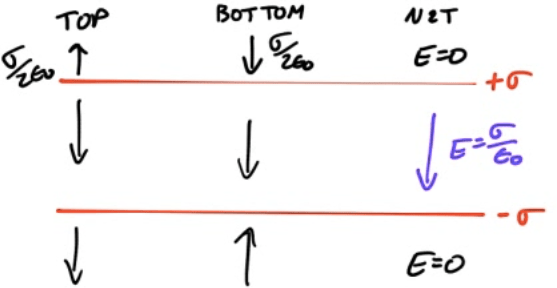
  • Find the electric field outside and between two oppositely-charged parallel planes or plates

    C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image068.png

Practice Question 4

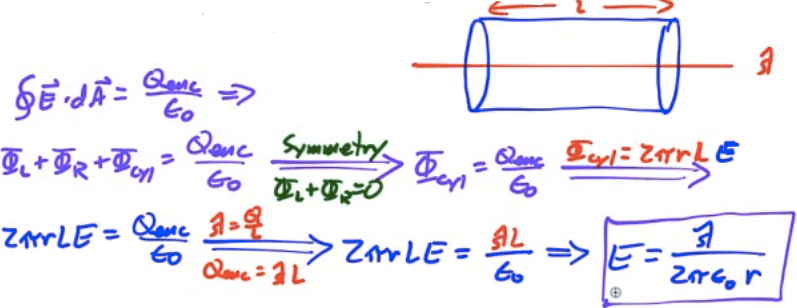
  • Find the electric field strength at a distance R from an infinitely long uniformly charged wire of linear charge density λ

    3 Zçrç.

2008 Free Response Question 1

a c A metal sphere of radius a contains a charge +Q and is surrounded by an uncharged, concentric, metallic shell of inner radius b and outer radius c, as shown above. Express all algebraic answers in terms of the given quantities and fundamental constants. (a) Determine the induced charge on each of the following and explain your reasoning in each case. i. The inner surface of the metallic shell ii. The outer surface of the metallic shell (b) Determine expressions for the magnitude of the electric field E as a function of r, the distance from the center of the inner sphere, in each of the following regions. i. ii. iii. iv.

(c) On the axes below, sketch a graph of E as a function of r. (d) An electron of mass me carrying a charge —e is released from rest at a very large distance from the spheres. Derive an expression for the speed of the particle at a distance 1 Or from the center of the spheres.

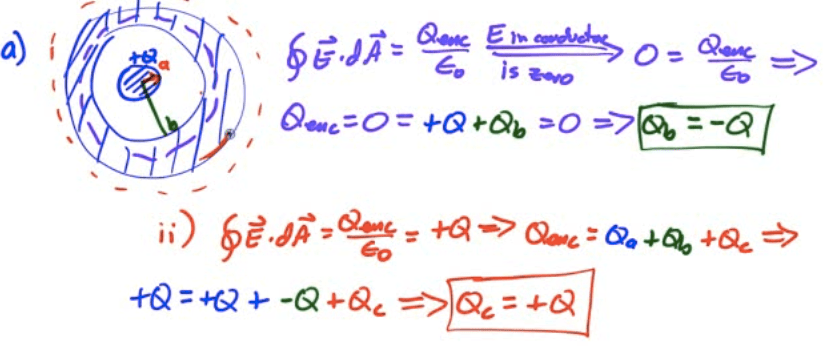
ナ : つ く = つ 2- イ : 十 0 く =

0

“ , ~ 0 + 丶 , 、 ” 0 冖 、

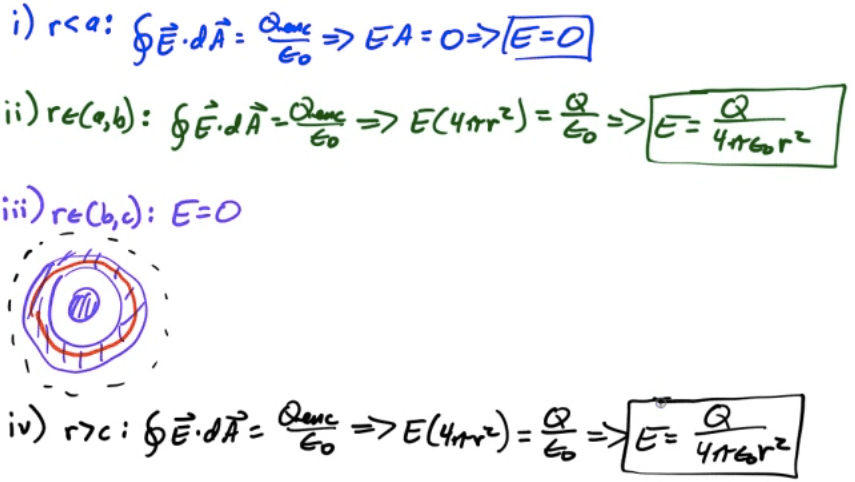
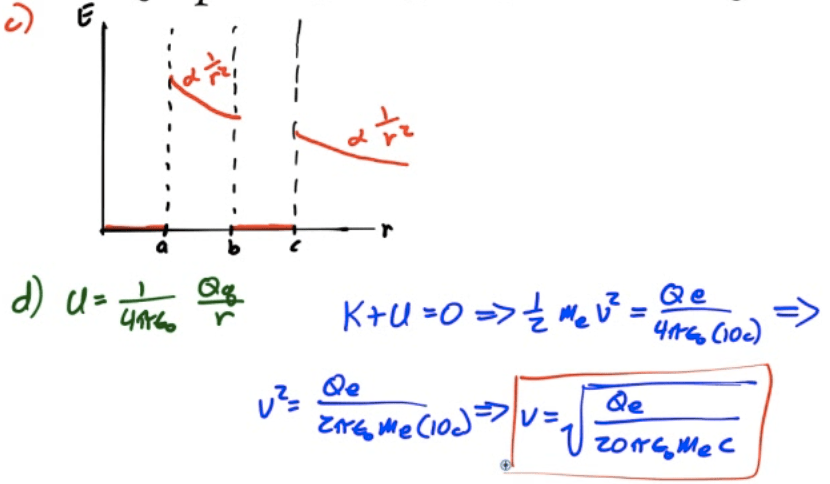
2011 Free Response Question 1

A nonconducting, thin, spherical shell has a uniform surface charge density on its outside surface and no charge anywhere else inside. (a) Use Gauss's law to prove that the electric field inside the shell is zero everywhere. Describe the Gaussian surface that you use. (b) The charges are now redistributed so that the surface charge density is no longer uniform. Is the electric field still zero everywhere inside the shell? Yes No It cannot be determined from the information given. Justify your answer. Now consider a small conducting sphere with charge +Q whose center is at corner A of a cubical surface, as shown below. (c) For which faces of the surface, if any, is the electric flux through that face equal to zero? ABCD CDEF EFGH ABGH BCFG ADEH Explain your reasoning. (d) At which corner(s) of the surface does the electric field have the least magnitude? (e) Determine the electric field strength at the position(s) you have indicated in part (d) in terms of Q, L, and fundamental constants, as appropriate. (f) Given that one-eighth of the sphere at point A is inside the surface, calculate the electric flux through face CDEF.

(a عو) ه المماهو اهعأة عل:»» عنا ومحل للره لعاه و- سح «محى - يه يخحة بيع اده لحتتتادد (ما وند . مسمقزلا عطد متلنسننبمة إي ـموهحط له لعمنسهه همهه مممهمما لمسولتمه C عف حا .لجتده سع ييهم (e ,AOfbABzb ععسافه:)A سد للكهم يلا غد سعمهس مههسعشد ه جسي مسمعظد صما سممعسه عددت م بكندسد، ا١:سمe م،»

C:\\266298A5\\73477446-49B2-471B-AFDD-BCD03931DCDD\_files\\image077.png

results matching ""

    No results matching ""